決定係数について　【相関係数と同じようで違うのです】

前回は回帰における正規方程式の意味するところを解説しました。

今回は回帰において重要な決定係数に関して解説します。

エクセルで散布図を作図すると、近似曲線を引くことが出来る機能があるのですがその適応度合いをみるためにR²を表示する機能はご存知でしょうか。

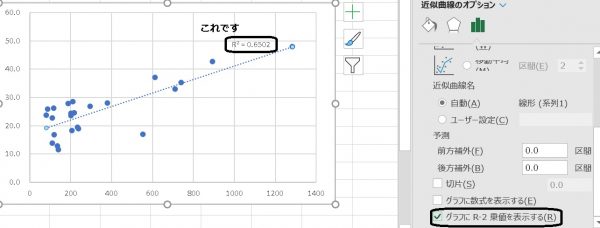
このR²のことを決定係数と呼びます。

「R²って相関係数と同じでしょ？」

• 相関関係とは何か？【公式からエクセルでの算出まで紹介します】

と思われる方もいらっしゃると思いますが、実は目的が異なります。

今回は決定係数の成り立ちから、相関係数とどのような違いがあるのかを紹介していきます。

こちらの本を元に解説しています。

基本統計学第4版

posted with ヨメレバ

宮川公男 有斐閣 2015年03月

楽天ブックス

Amazon

Kindle

動画でも解説しています。

統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ

決定係数を導こう！

各成分における分散

体重yと身長xの例で説明していきます。身長が高い人ほど体重が重いと考えられるので、ここには回帰関係があると考えます。

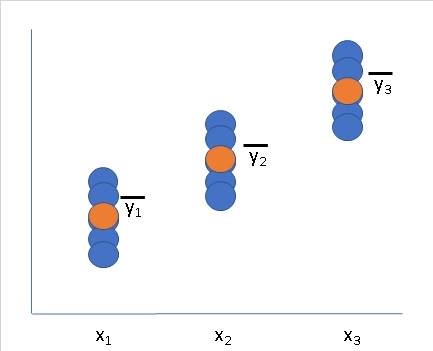
そんな中で分散を考えると、まず身長xを考慮せずにあるn人の集団の体重yの分散を考える場合、その式は

$$s_y^2=\frac{1}{n}\sum_{i=1}^{n}{(y_i-\overline{y})^2}$$

ただしはyの平均値です。

この数値は、この集団のすべての分散(=総分散)と言えます。

しかしその集団の中で、身長xに依存している体重yが存在する場合、

・身長に依存する体重

・身長に依存しない体重

がそれぞれ存在しているはずです。

ここで身長に依存しない体重を考えてみます。

この身長に依存しない体重の分散は、以下の式で表されます。

$$s_{y・x}^2=\frac{1}{n}\sum_{i=1}^{n}{(y_i-\overline{y_{xi}})^2}$$

ただしはx_iに対応する平均体重です。

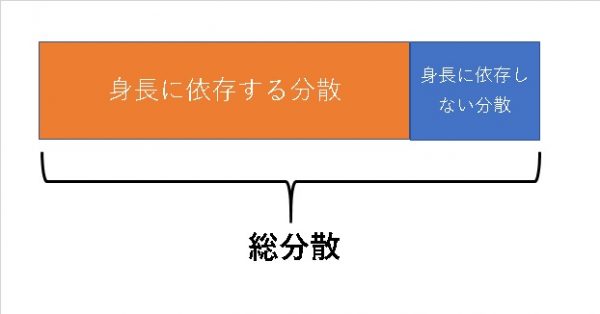
そして分散の加法性から、総分散から身長によって決定されない分散を引くと、必然的に身長によって決定される分散が導かれます。

$$s_r^2=s_y^2-s_{y・x}^2$$

以下のイメージを見て頂くと、分かりやすいかもしれません。

決定係数の算出

ここで身長xに依存する分散s_r²と全部の分散s_y²の比率を示すことが出来れば、分散のうちに身長xがどれだけ寄与しているかを知ることが出来ます。

つまり

$$r^2=\frac{s_r^2}{s_y^2}=1-\frac{s_{y・x}^2}{s_y^2}$$

で示されるr²は、全部の分散yのうちxによって決定される分散の割合を示す数値と言えます。

このr²を決定係数と言います。

決定係数は0≦r²≦1の間を動きます。

0の場合はxがyの値をまったく決定しないことを示します。

1の場合はxがyの値をすべて決定することを示します。

つまり0に近いとxと無関係になり、1に近いとxに決定される度合いが増えます。

決定係数は、その名の通りxによって、yが決定されるか否かを示した指標になります。

さて、この一定の範囲でxとyの依存度を示す数字として、別の代表的な指標が存在します。

そう、それは相関係数です。

この二つの指標は、非常に強い関連を持つ値同士でありながら、微妙に示している事象が異なるという間柄になります。

決定係数と相関係数の関係

相関係数は-1≦r≦1ですが、0と１の関係は同じです。

実は相関係数を2乗すると決定係数になります。逆に決定係数の平方根を取ると相関係数になります。

この場合相関係数の符号ですが、回帰式

$$y_a=a+bx$$

のbの符号と一致します。

2乗か否かだけの違いに見えますが、式のアプローチの仕方が異なります。

相関係数は4事象のうちの数値の集まり具合に注目しています。

決定係数は回帰式の変数xによる分散の比率に注目しています。

ここで注意が必要で、

・相関性を見る場合には相関係数を使う

・回帰式の当てはまり具合を見る場合は決定係数を使う

必要があります。

簡単に相関係数0.5という数値で考えてみます。

相関係数0.5というと中々相関性が取れていると言える数値と言えます(検定で見解が変わる可能性はありますが)。

しかしながら決定係数で考えると0.5を2乗するので0.25となります。かなり小さい数値です。

つまりこの場合は

「相関性はありそうだけど、回帰式での数値の予測は難しそう」

となります。

ここで相関係数と決定係数を混同して考えてしまうと

「相関係数で0.5で相関性は強そうだから回帰式で数値の予測も出来そうだ!」

と誤った結論を出してしまう可能性が出てしまうのです。

また、相関係数は-1～1の数字ですので、2乗する決定係数との関係は常に

|相関係数| ≧ 決定係数

となります。

これは単に相関性を示すよりも、yを導ける式(回帰式)の適合は厳しいという実態を良く表している関係性であると言えます。

まとめ

今回は決定係数の導出を解説しました。

相関係数が目的変数と説明変数の依存ぶりを示す値なのに対して、決定係数は回帰式の信用度を示します。

この辺りの区別がつかず、yとxの依存度を決定係数で計ってしまう人ってかなり多いと思います。

エクセルの近似曲線で簡単に表示されやすいですから。

故にこの辺りを明確に区別できるようになると、統計リテラシーが一つ上のレベルに上がります。

ぜひ決定係数と相関係数を使い分けて、正しい分析を実施しましょう。

コンテンツ紹介

昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。

そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。

しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。

そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。

youtubeでは登録者1万人の統計学のチャンネルを運用しています。

熊野コミチの統計とお仕事チャンネル

動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。

youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。

メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)

エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。

本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)

「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」

そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。

私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。

私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。

統計学を活かす 解析しやすい数値化のノウハウ

「いや、その前に使える手法を体系的に学びたいんだけど」

そんな方には、udemyの講座を推奨します。

メーカーの現役技術者による研究開発のための統計学

初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。

どの手法が結局使えますのん？という方はぜひこちらをお求めください。

こんな感じで、様々なコンテンツを展開しています。

今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。

ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。

twitter