統計学を用いてデータを分析する上では、分布の形状は非常に重要です。
正規分布でないのに、t検定を実施してしまった場合、正しい結果が得られなくなります。
ここで、重要になってくるのが正規分布でなくても分析出来る手法です。
今回はそんなノンパラメトリック分析の代表例であるマン・ホイットニーのU検定を紹介します。
マン・ホイットニーのU検定とは？
ノンパラメトリックで分析出来る理由
データの規則性を利用して、データを分析する統計学ですがノンパラメトリック(決まった分布ではない)なデータをどのようにして分析するのでしょうか。
その秘密は順位にあります。
2つの集団に差が無い場合、集団を混合させて順位をつけたら、元の2集団に所属したデータの順位の合計は似た値になるはずです。
もしこれに偏りが生じた場合、データに差が有ると判断出来ます。
これがノンパラメトリック分析の主な原理です。
詳細は、以下の記事を参照ください
マン・ホイットニーのU検定
2つの集団のサンプルサイズが、n1、n2である場合以下のような検定統計量を算出します。
$$U_1=n_1n_2+\frac{n_1(n_1+1)}{2}-R_1$$
もしくは
$$U_2=n_1n_2+\frac{n_2(n_2+1)}{2}-R_2$$
R1とR2はそれぞれの順位の総和です。
この内の小さな方の値を使います。
このUですが、以下の図のような考え方になります。
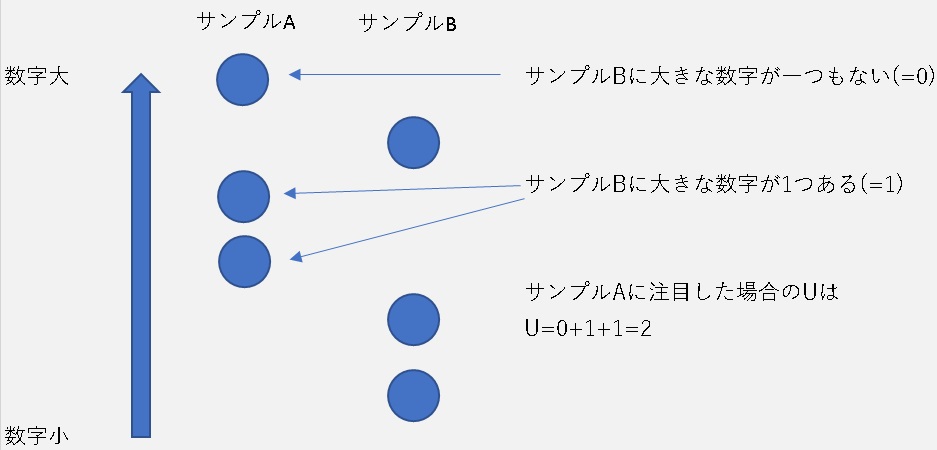
片方の集団に注目し、相手の集団と比較して大きな数字の有無とその個数をカウントし、総和します。
そして2集団それぞれのサンプルサイズが20以下であれば、検定表でチェックします。検定表の数字よりもUが小さければ有意と判断します。
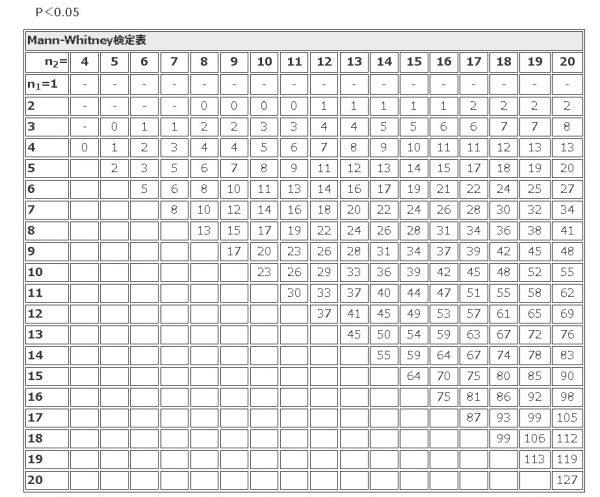
それを超えた場合は、Uの平均値と分散値を算出します。
Uの平均値と分散値は正規分布に従うために、そこからZ検定を実施します。
$$μ=\frac{n_1n_2}{2}$$
$$σ=\sqrt{\frac{n_1n_2(n_1+n_2+1)}{12}}$$
$$Z=\frac{U-μ}{σ}$$
Z検定については以下の記事をご覧ください。
独特な考え方ですが、そこまで厳密に覚えなくても良いです。
EZRで簡単に実施出来ます。
EZRでマン・ホイットニーのU検定を実施しよう!
こちらのデータを分析してみましょう。
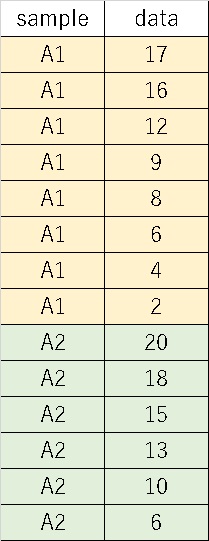
実際にやってみよう
EZRを開き、統計解析タグのノンパラメトリック検定を選び、2群間の比較(Mann-WhitneyU検定)をクリックします。
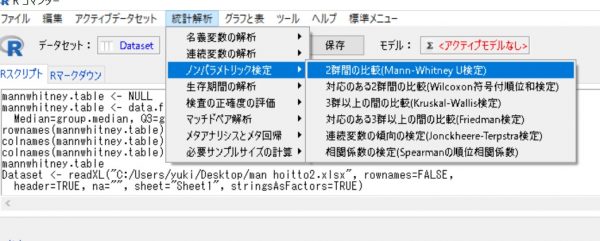
そして、目的変数(分析する値)と比較する群(集団の名前)を選択肢、OKをクリックします。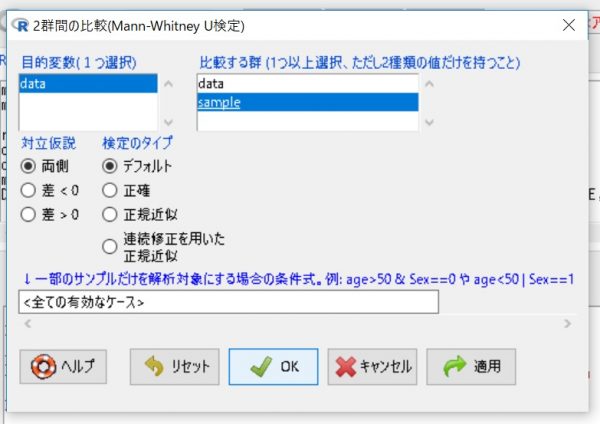
これで、手順は完了です。
結果を見てみよう
結果は以下のようになります。
P値は0.155となっています。有意水準α=0.05とした場合、帰無仮説(2つの集団は等しい)を棄却出来ません。
よって、有意差があるとは言えないという結論となります。
まとめ
マン・ホイットニーのU検定を用いれば正規分布していなくても、平均値の差の検定を実施することが出来ます。
また、正規分布をしていてもかなり高い検出力を発揮すると言われいるため、基本的にEZRでこの検定を実施していれば特に問題ないとも言えます。
ただ一点、分散が等しい者同士でないと、検出力が下がるそうです。
その場合はwelchのt検定の方が有利です。
ただ、複数の検定(F検定や正規性の検定)を重ねると検定の多重性の問題から、検出力が悪化するので、データの性質をよく知ったうえで適切な検定を実施するようにしましょう。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか？
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう
コメント