会社の先輩が先日セミナーを受けてきたのですが、本人曰く
「なんか式がいっぱい出てきて、よく分からなかった」
と言って困っていました。
一応テキストを見せてもらったのですが、ηだの、Θだの一見難しそうなギリシャ文字で変数が構成されていますが、よくよく見るとそんなに難しいものとは思えませんでした。
しかしながら、学生時代に数列だの微積分だので躓き、苦手意識を持ってしまった人はもしかしたら数式を見た瞬間に
「あっ数式だ。もうダメ、分かんない」
とアレルギー反応を起こしてしまうものなのかもしれません。
そうだとすると、かなり勿体ないと思います。
ちなみにその先輩は、現場からの叩き上げで、当該の現象についての理解度は高い人です。
ただ、現場からの叩き上げや、人員が少ないからと文系だった人間が開発等の部署に異動して、数式を相手どらないといけないシチュエーションもあると思います。
そんな時、苦手だからと言って数式を避けていては技術としては、やっていけなくなります。
特に現場から異動してきた人は、元々現物に対しての経験値が高く、理解度もすさまじいものがあるので、数式が理解できないという事実は、本人だけでなく、会社にとっても損失です。
という事で今回は、『クーロンの法則』を例に数式アレルギー攻略法を紹介いたします。
動画でも解説しています。
数式を見てみよう

まず、クーロンの法則ですが、式はこんな形です。
$$F=k\frac{q_1q_2}{r^2}$$
Fは電荷間の力、qは荷電粒子の電荷量、rは荷電粒子間の距離、kは比例定数を表しています。
何を言っているか分からないと思います。数式アレルギーの人からすれば
「あーやっぱ分からんっ」
となっているものと思います。
ですが安心してください。数式には見極めるポイントがいくつかあります。
そこを一つ一つ抑えていけば、この式をはじめサラリーマンが触れる程度の数式については解釈することが出来ます。
ポイント1:アウトプットとインプットを見極める
まず、式の関係を見てみましょう。
基本的にイコール(=)の左側(左辺)にくる数字がアウトプットで、右側(右辺)にくる数式がインプットです。
つまり、アウトプット”F”を求めるためには、右辺の各項目に数字をインプットすれば良いということを、この式は示しています。
ポイント2:定数は切り捨てる
次に定数と変数を見極めましょう。
定数と変数とは
定数:どんな状況でも変わらない数
変数:状況によって変わる数
定数はどのような状況でも変化しないので、無視してしまいましょう。
この場合、kが定数になります。
定数は神様が決めたようなものなので、なぜそのような数字になるのかは誰にも分かりません。
そんな数字を相手にしても時間の無駄です。
ですので、ここであなたが相手すべき数字は変数qとrになります。
ポイント3:分子か分母か?
この式ではqが分子、rが分母に来ています。
$$\frac{q_1q_2}{r^2}$$
このように分数になっている場合は、分子にくる変数はアウトプットを大きくし、分母にくる変数はアウトプットを小さくするとだけ考えてみましょう。
この場合
・q1またはq2はFを大きくする
・rはFを小さくする
ことになります。
このようにインプットする変数が、アウトプットを大きくするのか、小さくするのか、という視点は式を把握する上で極めて重要な考え方です。
ポイント4:乗数がその数式の主役
乗数とは数字や変数の右上にくっついている数字のことです。
この乗数は、ついている対象の数字や変数をその乗数の回数掛け算するという意味を示しています。
「それが一体どうした」
と言われそうなものですが、この乗数は数式を把握するうえでかなり重要なポイントです。
乗数がついていると、アウトプットは爆発的に変化します。
例えば
$$y=x^2$$
という式があったとします。これはxを2回掛けた数字がyという意味です(2が3になると、3回掛けた数字がyになります)。
このxを1,2,3と大きくしていくと、アウトプットであるyは爆発的に大きくなっていきます。
x=1 のときy=1
x=2のときy=4
x=3 のときy=9
x=4 のときy=16
グラフにすると、
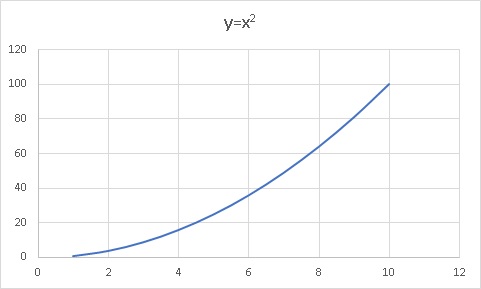
こんな感じです。
ここまでの説明で分かって頂けたかと思いますが、この乗数がついている変数はアウトプットに対する影響度が他に比べて大きいのです。
つまり、この乗数がついている変数はその式の主役であり一番訴えたいことなのです。
クーロンの法則の場合
$$\frac{q_1q_2}{r^2}$$
rに2乗がついています。つまり、『rが力Fに大きな影響を与える変数である』ということをこの式は訴えているのです。
式を解釈してみよう!
これまでを整理すると、
・q1、q2はFを大きくする
・rはFを小さくする
・rは2乗になっているので、q1、q2以上にFに対する影響度が大きい
以上がクーロンの法則が示している内容です。
一見無機質に見えた数式が、とても簡単に見えてきませんか?
以上が数式を理解するポイントになります。
まとめ
社会人になっても、業種によっては数式は付きまとってきます。
しかも、ある日突然異動になって勉強が必要になるという状況も大いにあり得ます。
ですが、今回紹介したアプローチをとればある程度の数式は理解出来るようになります。
また、元々数式が得意な人も、逆に
「数式が分からない人には、こう説明すれば良いんだ」
という風に、苦手な人に説明する観点になると思います。
物事を簡単に説明出来るスキルというものは、非常に重宝します。
これを元に勉強会を実施すれば、プレゼン能力も向上して、あなたの市場価値の向上にもつながるはずです。
数式が苦手な人も、得意な人も、ぜひこの思考法を使用、伝授してみて下さい。




コメント