検定は平均値やばらつきの差が本当に有意かどうかを示してくれる、非常に便利なツールです。
おそらく、初めて検定を知った人は
「これはスゲェ!今度から差があったら、無かったりが明確になるじゃん!!」
と驚いたハズです。
私はそうでした。
ですが、もし「差が無いことは言えない・・・」としたら?
「詐欺じゃねぇか!!」と怒髪天を突く方もいらっしゃるでしょう。
私の髪は天を突きましたよ。
そう、実は検定において差が無い事を積極的に採択する事は出来ないのです。
という事で本日は、なぜ差が無いと言えないのか、これを解説していきます。
一応先に述べておきますが、差が無い事を積極的に述べたい、そんな方法を知りたいという方は、こちらの記事をご覧ください。その方法論を提案していますので。
ただ本記事で、なぜ差がない事を言えないのか知っておいた方が良いとは思います。誤用がなくなりますので。
検定で差がないことを言えない?

検定を復習しましょう
まず検定という手法を振り返ってみましょう。
詳細は以下の記事を参照してほしいのですが、
ざっくり述べると、
H0:帰無仮説を設定
H1:対立仮説を設定
有意水準αを設定
検定を実施
αより小さな確率値が出れば、H1を採択。そうでなければH0で保留
といった流れで実施されます。
分布を使って検定を考えてみよう
それでは次にこの検定という作業を分布に起こして、確認しましょう。
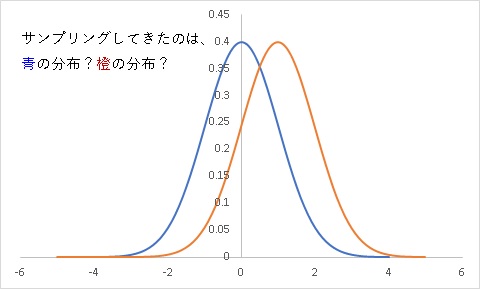
青の分布を本当のサンプリング元、橙の分布を青と差があるサンプリング元とします。
その場合は、検定というものの帰無仮説/対立仮説というものは
H0:青の分布からサンプリングした
H1:橙の分布からサンプリングした
ということなのです。そして有意水準を決めるという事は、
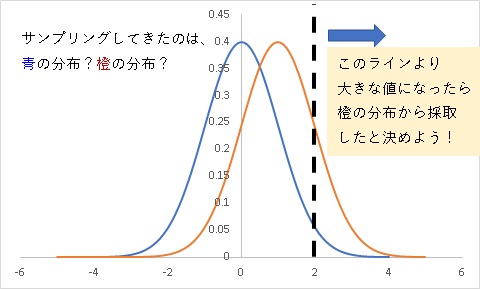
このような、あるラインを越えたら橙の分布からサンプリングした事にしようという、そのラインを引く作業を指すのです。
見てもらえたら分かるように、このラインを越えても青の分布から採取した可能性もわずかばかり残ります(有意水準と一致します)。
これが正に、第一種の過誤そのものなのです。
「差が無い」という結果を考えてみよう
ここから差が無いという状況について、考えていきます。
もう一度青と橙の分布の図を見てみましょう。
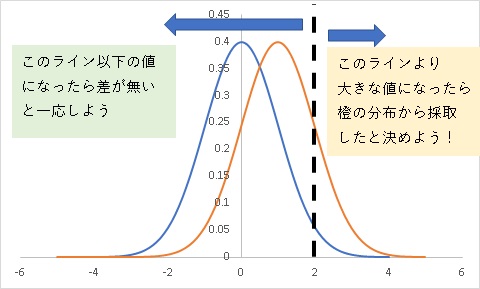
先程のラインより大きくなったら橙の分布とする、という事はその逆は
ラインより小さくなったら青の分布(つまり差が無い)とする、という事です。
さてここで注目してほしいのが、ラインより小さい側の青と橙の分布です。
青の分布は当然ですが、橙の分布もかなりの割合存在しているのです。
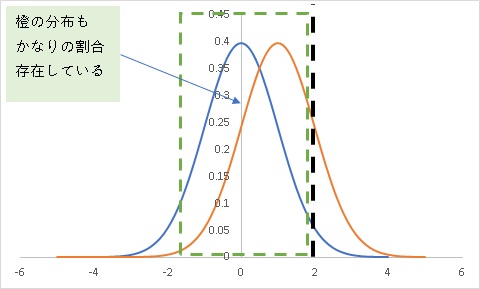
これでは、ラインより左側なら青の分布から採取してきたと、自信を持って言及出来ないのは当然です。
つまり、これが帰無仮説、差がないという事を積極的に言及出来ない理由になります。
これ、実は青と橙の分布の位置関係でかなり意味合いが異なってきます。
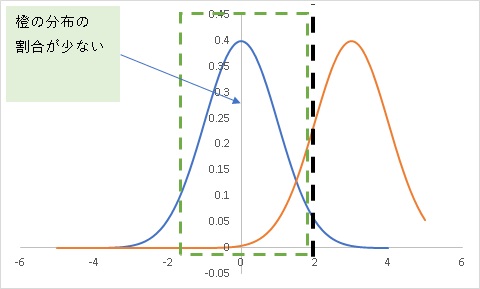
このように青と橙の分布の距離が離れていると、帰無仮説が棄却出来ない場合、かなりの確率で青の分布からサンプリングしてきたと言えるのです。
この発想は効果量という考え方になり、サンプルサイズの決定に関わる非常に重要な考え方です。
効果量をあらかじめ設定した上で、検定を行えば帰無仮説を積極的に採択出来ます。差が無いという事を積極的に採択出来ます。多分。
ただ、色々使ってみると、この方法は結構難しいというのが私の印象です。
まとめ
検定は、差が無いという結果を積極的には採択しにくい手法です。
理由は分布の重なり具合によっては、有意水準より大きい場合でも別分布からサンプルを採取してきた可能性が高いからです。
実際に差が無いことを採択するには、サンプルサイズを設計して効果量を考慮するか、誤差と技術的な差の違いを利用する方法が存在します。
このような方法を使えば、検定で差が無いという状況にも対応できると思いますので、ぜひ試してみて下さい。
当サイトで学習/実践を繰り返して統計力、仕事力、開発力が伸びてきたら、更に上の職場にステップアップというのも一つの手です。
こちらでは、エンジニア専門の転職活動を支援しています。ぜひ活用してみて下さい
先端技術・イノベーション領域に強いエンジニア転職支援サービス【Kaguya】無料会員登録



コメント