エクセルで散布図を作って直線関係を描いたときには、当然相関性を分析しますよね?
もし何それ?という方いらっしゃったら、まずはこちらの記事をご覧ください。
その相関関係が綺麗に表現されている時、つまり
相関関係を見たときに相関性が極めて1(もしくは-1)に近い場合
「これだけ一直線なら片方の数値が決まったら、もう一方の数値を算出出来るようになるんじゃね?
といった発想が出てくる方もいるでしょう。
その発想を実現させるものが回帰分析です。
エクセルでも相関関係のグラフを作ったうえで、近似直線で直線を引き数式を表示を選択すると回帰関係の式が簡単に出てきます。
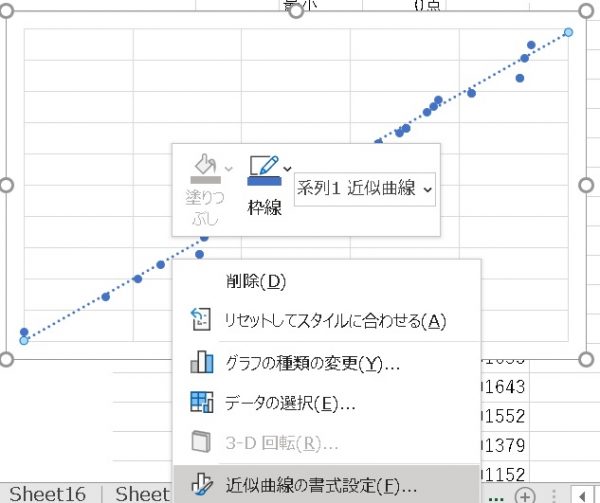
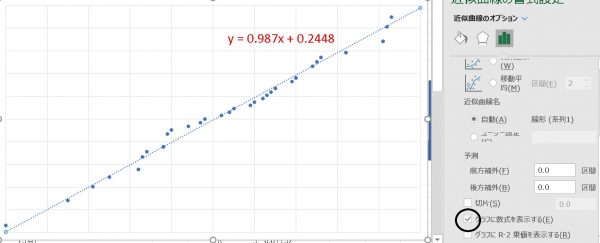
「よっしゃ、出し方は分かった、もうお前に用はねぇ、あばよっ!」
と式の出し方が分かればいいという方は、ここで踵を返してもらっても大丈夫です。
ですが、どういう風なロジックでこの式が算出されているのか知りたいというのであれば、お手数ですが、もう少々お付き合いくださいな。
この回帰分析の数式は見た目の印象と裏腹に、導出が結構難しいです。
ですが扱う道具に関して多少なりとも原理は知っておかないと誤った使用をして、間違った判断をしてしまう可能性が出てきます。
ですので知識としてだけでも、把握した上で扱っていきましょう。
ちなみに今回の解説はコチラの本を参照に行います。
より詳細に知りたい方は、ぜひ手に取ってみて下さい
回帰分析とは何か?

条件付き平均値と回帰関係
まずは、回帰関係というモノを今一度考えてみます。
身長と体重の関係で考えてみましょう。
基本的には身長が高い人は概して体重が重く、身長が低い人は概して体重が軽くなるというのは、経験的に実感のあることだと思います。
ですが、すべての人において身長と体重の関係が当てはまるかと言えば、
それはない
となることも、同様に経験的に実感があることと思います。
これは以下のように言い換えることが出来るということです。
身長が高い人は平均的に体重が重く、身長が低い人は平均的に体重が軽い
このように異なる身長(x)に対して、異なる平均体重(![]() )が対応するという関係を
)が対応するという関係を
身長(x)に対する体重(y)の回帰関係
と言います。
ここでのポイントはあくまでxに対してのyではなく、yの平均値![]() が対応するということです。
が対応するということです。
このような一定のxに対応する![]() のことを、条件付き平均値と言います。
のことを、条件付き平均値と言います。
これはxという値には色々なyが対応して、その中ではxに相関しないyもいるが、平均で見たらyはxに対応しているということを指しているという事です。
図で表すとこんな感じです。
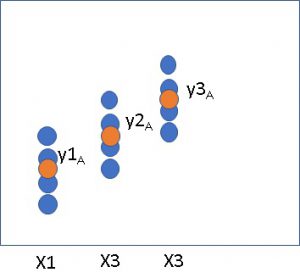 式で表すとこうなります
式で表すとこうなります
$$\overline{y}=f(x)$$
ちなみに、一般的には身長から105を引くと標準的な体重になると言われていますが(まぁ私は初耳でしたよ)、これも回帰関係を意味しており式で表すと
$$平均体重\overline{y}=身長x-105$$
これは通常の関数とは異なる関係です。
関数関係とはあくまでも一つのxに対して一つのy(平均ではない)が決まる関係
$$y=f(x)$$
のことを言います。
線形回帰
回帰関係にも様々なものがありますが、一般的に用いられるものは一次式(つまり線形)の
$$\overline{y}=a+bx$$
ただしa,bは定数です。
例えば先ほどの身長と体重の回帰関係の場合は
a=-105, b=1
になります。
このようなaとbのことを回帰パラメータと言います。
回帰関係の式を見出すということは、回帰パラメータを算出することを意味するのです。
という事で、ここから回帰パラメータの算出方法の解説に入ります。
書いている人間がウンザリするくらいに、数式いっぱい出ます。
多少我慢してお付き合いください。
回帰パラメータを算出しよう!

最小二乗法
少し図を交えて解説していきます。
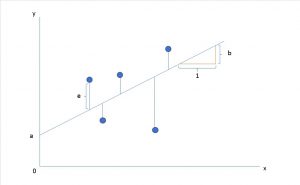
回帰関係ではxとyが直接関連する関係ではありません。
xと![]() の関連する関係です。
の関連する関係です。
なので一次式的な回帰関係をこのように図示しようとすると、このようにそれぞれの値の集まりの中心を通るような直線を引くのが、一番筋の通ったものと言えます。
中心を通るというのはすなわち、直線と各値の差eが最小になるような書き方を言います。
eの事を偏差と言います。
eを回帰式を交えた表現で表すと、
$$e=y_i-\overline[y]=y_i-(a+bx)$$
です。
各yにつき偏差は存在するので、全ての偏差を盛り込むなら偏差の総和を出すのが良さそうです。
しかしながら、偏差の総和は必ず0になってしまうので、2乗した偏差の総和、偏差平方和で表現するとします。
$$S(a,b)=\sum_{i=1}^{n}{(y_i-(a+bx_i))^2}$$
そしてこのS(a,b)が最小になるようなa,bを求めれば、晴れて回帰式が完成するという訳です。
このような方法を最小二乗法と呼ぶのですが、名前はまぁどうでも良いです。
私もよく忘れますし。
さて、ここからどうすれば良いのか?
このS(a,b)を微分します。
2次方程式を微分すると、接線の式が求まります。
そして2次方程式の極小点(つまりS(a,b)が最小になる、我々が目指す部分)の接線は0になります(高校で習ったハズ、思い出して!)。
実際にはa,bそれぞれに対して偏微分するので、式はaで微分した式とbで微分した式の2つが出てきます。
左辺が0になった式が2つ出てくるので、後は連立方程式を解けば、a,bが求まるよって訳なんです。
解いてみよう
偏差平方和
$$S(a,b)=\sum_{i=1}^{n}{(y_i-(a+bx_i))^2}$$
さてこれを偏微分すると
$$\frac{∂S(a,b)}{∂a}=\sum_{i}{2[y_i-(a+bx_i))]}(-1)=0$$
$$\frac{∂S(a,b)}{∂b}=\sum_{i}{2[y_i-(a+bx_i))]}(-x_i)=0$$
となります。ここから更に整理しますと以下のようになります。
$$① \sum_{i}{[y_i-(a+bx_i)]}=\sum_{i}{e_i}=0$$
↓
$$①’ na+b\sum_{i}{x_i}=\sum_{i}{y_i}$$
$$② \sum_{i}{[y_i-(a+bx_i)]}x_i=\sum_{i}{e_i}x_i=0$$
↓
$$②’ \sum_{i}{x_i}+b\sum_{i}{x_i^2}=\sum_{i}{x_iy_i}$$
となります。この①’及び②’の二つの式はa,b以外のパラメータはデータから計算されるものなので、結局a,bについての連立一次方程式になっており、これを解くとa,bが求まります。
これらの式の意味するもの
ここで、正規方程式が何を示しているのかを見ていきましょう。
①及び②は導出の過程で導いたものですが、a及びbが満たすべき条件を示したものです。
まず①が意味するものですが、これは
・回帰直線からの偏差eの合計が0
であることを示しています。
回帰直線の上側に外れているプラスのeと下側に外れているマイナスのeが互いに打ち消しあう位置づけに、回帰直線を引くという条件を表しているのです。
また①’をnで割ると以下の式になります。
$$\overline{y}=a+b\overline{x}$$
これはxが![]() であるときは
であるときは![]() であること、すなわち回帰直線は(
であること、すなわち回帰直線は(![]() ,
,![]() )を必ず通ることも条件に組み込まれています。
)を必ず通ることも条件に組み込まれています。
次に②が意味するものですが、
・回帰からの偏差eiとそれに対応するxiの積の合計は0
というものです。この条件が加わることで、(![]() ,
,![]() )を中心とした無数の回帰直線候補を一つに絞ることが出来ます。
)を中心とした無数の回帰直線候補を一つに絞ることが出来ます。
まとめ
おさらいとして回帰直線の満たすべき条件とは
・回帰直線からの偏差eの合計が0
・回帰直線は(xA,yA)を通る
・xiと回帰からの偏差eiとそれに対応するxiの積の合計は0
この条件を満たす回帰直線は一つだけになります。
最終的な式だけを見るとなぜそうなったのか分からないものですが、このように導出の過程を見ていくとなぜそのようになるのか分かるようになります。
式の意味が分かると、分析した結果がどのように計算されたのか、どの値が起因してそのような結果になるのかが分かるようになり、考察の精度が増します。
統計は便利なツールですが、それに振り回されることなく使いこなしましょう。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント