管理図は工程の日常管理や、現場の状況を分析するのに非常に使えるツールです。
この管理図ですが、作る時に最も重要と言えるのが管理限界値です。
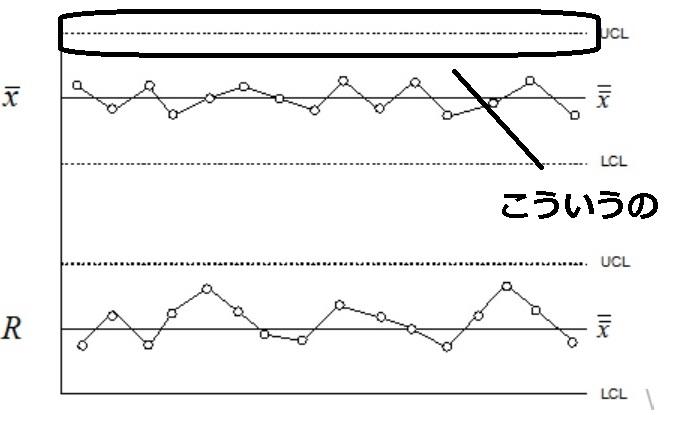
この管理限界を外れるかどうかで異常かどうかを判断するためです。
この管理限界は3σを基準に線引きするという事になっていますが、様々な書籍では係数を用いた線引き方法がよく提示されているのです。
単純に3σを引いてはダメなのでしょうか?
という事で今回は係数で算出した場合と標準偏差×3(=3σ)で、管理限界値に差があるのかどうかを確認してみました。
結論としては、殆ど差がありません。
管理図の管理限界値について

管理図って何?
このようなページに検索でたどり着いた方には、必要ないかもしれませんが一応管理図について簡単に解説いたします。
管理図とは、工程の状態に異常が無いかを日々管理する為に作られたツールで、基本的には
・日々N=5程度製品を抜き取りデータを測定
・N=5の平均値や範囲をプロットする
・定めた管理限界値から外れていなかったらOK
とするシンプルながらタイムリーに工程管理を行う事が出来る素晴らしいツールです。
詳しくは以下の記事を参照してください。
3σを管理限界としている
管理図を作るうえで、最も重要なのは管理限界値です。
管理限界値の引き方で、日々のデータの解釈が変わってしまうからです。
この管理限界値ですが、原則としては規格の中心CL![]() に対して平均値
に対して平均値![]() の標準偏差の3倍、つまり3σを上下に引きます。
の標準偏差の3倍、つまり3σを上下に引きます。
![]() ±3σが上下限の管理限界値なのです。
±3σが上下限の管理限界値なのです。
この理由としては、この管理限界から外れる確率が極めて低い(0.3%)という事が正規分布の性質から言える為です。
元のデータの分布に関係なく、平均値の分布は必ず正規分布になります。
これを中心極限定理と呼びます。
管理図の強みは、この統計的な裏付けにあると言えます。
平均値のプロットなので、元のデータに関係なく正規分布を適用出来、その為3σで管理するという事を一義的に決める事が出来るのです。
係数を使った計算法
(不偏)標準偏差を求める式は
$$σ=\sqrt{\frac{\sum_{i=1}^{n}{(x_i-\overline{x})^2}}{(n-1)}}$$
なんですが、管理図では別途範囲Rと特殊な係数を使った管理限界値の算出方法が存在しています。
内容は
平均値のUCL/LCL
$$UCL=\overline{\overline{x}}+A_2\overline{R}$$
$$LCL=\overline{\overline{x}}-A_2\overline{R}$$
範囲RのUCL(抜き取り数が6以下の場合はLCLを算出しない)
$$UCL=D_4\overline{R}$$
ただし、
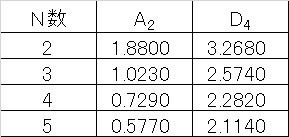
とA2やD4は採取したサンプルの数によります。N=5の場合は
A2=0.5770
D4=2.1140
になります。
なぜこんな方法をわざわざ取るのでしょうか。
それは、管理図が成立した時期を考える必要があります。
管理図を作ったシューハート博士は20世紀前半(1967年没)の人物です。
ゆえに当然現場にパソコン(もといコンピューター)などおいそれと置いてある時代ではないのです。
標準偏差はエクセルを使えば、簡単に算出出来ますが、手計算ではかなり手間がかかります。
各値を平均から引いて、それぞれ二乗して、全て足し合わせて、自由度で割って、平方根をとる。
こんなの日々の管理でやっていられないのです。
その点、係数を使ったこの方法であれば、算出するのは平均と範囲(最大-最小)だけになるので、現場でも簡単な電卓レベルで計算出来ます。
つまりコンピューターがない時代には、この方法で3σの計算を簡略化する必要があったという訳です。
係数による推定と3σを比較しよう

係数で管理限界値を計算しよう
実際に係数を使った方法で3σを計算してみましょう。
数字は以下を使ってみます。
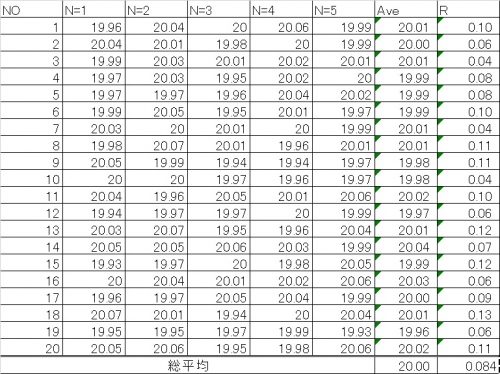
まず平均値のUCL/LCLです。
全体の平均値![]() は20.00
は20.00
範囲の平均![]() は0.08
は0.08
になります。なのでUCL/LCLは
$$UCL=\overline{\overline{x}}+A_2\overline{R}=20.00+0.5770×0.08=20.05$$
$$LCL=\overline{\overline{x}}-A_2\overline{R}=20.00-0.5770×0.08=19.95$$
になります。
そして、範囲のUCLは
$$UCL=D_4\overline{R}=2.1140×0.08=0.18$$
になります。
3σと比較しよう
この係数で算出した管理限界値を標準偏差×3と比較してみましょう。
というのも、
・本当に標準偏差×3に近い値なのか
・N>6のときの係数が分からないから係数法以外にも有効な手段を知っておきたい
というのが結構気になるのです。説としては係数による計算は3σの推定値とされていますが、実際に標準偏差×3と比較しないと自信が持てません。
という事で、標準偏差×3をそれぞれ出してみました。
標準偏差×3での平均値のUCL/LCLは
UCL
$$\overline{\overline{x}}+3σ=20.00+3×0.019=20.06$$
LCL
$$\overline{\overline{x}}-3σ=20.00-3×0.019=19.94$$
標準偏差×3でのRのUCLは
UCL
$$\overline{R}+3σ=0.08+3×0.029=0.17$$
一覧にすると、
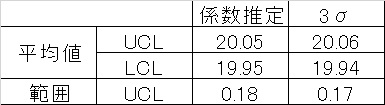
ほぼ同じ値を示しました。この程度の差なら同じ工程でのデータばらつきで生じ得るでしょう。
今回初めて試みたのですが、ここまで一致するとは思いませんでした。
逆に係数と範囲の値で3σをここまで予測した昔の人がスゴい・・・
ですが、やはりここまで一致となると、PCが現場に当たり前に存在する今となっては係数を使うよりもエクセルで標準偏差を算出した方が、係数のN数の制限を受ける事も無いので簡便かつ実用的であると言えるでしょう。
3σを算出する時の注意点
管理限界値の3σはふつうにデータの標準偏差を使う事で何とかなりそうです。
ですが、1点注意点があります。
それは平均値![]() の標準偏差を使うという事です。
の標準偏差を使うという事です。
というのも、管理図のClやUCL/LCLは平均値の正規分布を想定しています。
先述したように生データの分布とその平均値の分布は形状が違うのです。
つまり、生データの標準偏差と平均値の標準偏差は一致しないという事です。
実際に計算した値を並べるとこうなります。
生データのσ:0.038
平均値のσ:0.019
この値で管理限界値を求めると

このように、係数による推定値とも、平均値の3σともかけ離れた管理限界値になります。
これは日々の管理を誤る可能性が出てきます。
気を付けて下さい。
まとめ
管理図の管理限界値は総平均の±3σです。
これは平均値の中心極限定理と正規分布の性質を利用しています。
そして、管理限界値を算出する方法には3×標準偏差と係数による推定の2つが存在します。
どちらも同じような値を示しますが、エクセルが標準配備されている昨今は標準偏差から計算する方法の方が簡単で、幅広い状況にも対応できるのでオススメです。
今まで係数を使った方がいいのか、N>6だったらどうしようと迷っていた方はぜひこの方法を活用してみて下さい。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント
以下のことを教えて下さい。
①Xbar管理図で管理限界線に±3σを採用した場合、R管理図の管理限界線はRbar+3σ(Rbarの標準偏差)で良いのでしょうか?
②CpやCpkを求める時は全データの標準偏差を採用するのでしょうか?
それとも、Xbarの標準偏差を採用するのでしょうか?
1はその通りです
2は全データです。xbarの標準偏差ではありません。