統計を勉強していると、頻繁に期待値というものに遭遇します。
サラリーマンとしては、正直使わないなぁと思いする―していると重要な場面で解説に期待値が潜り込んだりして理解を阻害したりします。
という事で今回は、平均値と分散を期待値で表す場合及び期待値の式変形について解説します。
期待される数字とは?
コイントスで考える
例で考えてみます。
3枚のコインを投げる場合、表の出る枚数をxとするとxは0,1,2,3のいずれかの値を取ります(このようなxを確率変数と呼びます)。
この場合、それぞれのxの発生確率P(x)は以下になります。

例えば1000回(n)コイントスをするとします。その場合各xの回数nP(x)は
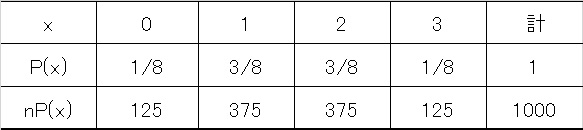
こうなります。そして1000回の実験で表の出る枚数はx×nP(x)の総和になりますから
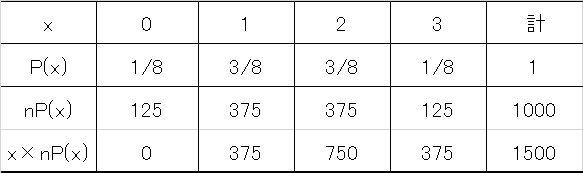
と1000トスして1500枚表が出ます。ゆえに1500回表/1000トス=1.5回表/トスが出る計算になります。
この1.5回は必ずしも出る確率ではありませんが、最も期待できる数字ではあります。
これが期待値です。
平均値≒期待値
期待値は最頻する数字であり、平均値と一致します。
数式で表現すると期待値E(x)は
$$E(x)=\sum_x{xP(x)}$$
で表現されます。先ほどのコイントスの例では
$$E(x)=\sum_x{xP(x)}=0×\frac{1}{8}+1×\frac{3}{8}+2×\frac{3}{8}+3×\frac{1}{8}=1.5$$
になります。また1,2,3,4,5,5という集団の場合の期待値は
$$E(x)=\sum_x{xP(x)}=1×\frac{1}{6}+2×\frac{1}{2}+3×\frac{1}{6}+4×\frac{1}{6}+5×\frac{1}{6}+5×\frac{1}{6}=3.3$$
になりまうs。これは
$$P(x)=\frac{1}{n}$$
の場合と一致します。
期待値と平均値は同じ値ですが、特に区別する場合には期待値には確率の考えが入っており、平均値には確率の考えが入っていないと考えます。
故に正規分布における平均値というのは、期待値と言った方が適切なのです。
偏差の期待値が分散
分散は平方した偏差の平均値です。
故に平方した偏差の期待値が確率の考えが入った分散になります。
偏差は
$$偏差=x-\overline{x}$$
ですので、その期待値である分散σ2は
$$σ^2=\sum_x{(x-\overline{x})^2P(x)}$$
になります。先ほどのコイントスの場合
$$σ^2=\sum_x{(x-1.5)^2P(x)}=(0-1.5)^2×\frac{1}{8}+(1-1.5)^2×\frac{3}{8}+(2-1.5)^2×\frac{3}{8}+(3-1.5)^2×\frac{1}{8}=0.75$$
となります。また、計算しやすくするためこのような式でも表現されます。
$$σ^2=E(x^2)-E(x)^2$$
他の統計学的手法を導出するときに、頻出すると思いますのでこの形も知っておいた方が良いです。
期待値の性質
サラリーマンが期待値を勉強する理由
私自身期待値を仕事に持ち込んだことがありません。
私のようなサラリーマンにとって統計学はあくまでツールであり、期待値に対してそこまで深く理解しておく必要があるとは思っていません。
ですが、ツールを使いこなすために勉強する為に、ちょいちょい期待値が顔を出すので何とかやり過ごす必要はあるわけです。
ということで、とりあえずこれから期待値の式変形の決まり事を列挙します。
暗記する必要もありませんが、期待値が出た際はぜひ照らし合わせてみて下さい。
今までよりかは、理解しやすくなるはずです。
期待値の性質一覧
cを定数、u(x)、v(x)を確率変数xの関数とした場合、期待値は以下のような性質を示します。
$$E(c)=c$$
$$E(cx)=cE(x)$$
$$E(cu(x))=cE(u(x))$$
$$E(u(x)+v(x))=E(u(x))+E(v(x))$$
これらを把握しておけば、統計学の導出で期待値が出てきてもなんとか読み進める事が出来ると思います。
まとめ
期待値は重要な考えではありますが、特に我々のように仕事でツールとして使う場合は利用することはないでしょう。
ですがツールを理解して使いたいが為に、「そこまで必要ないだろ」というような所で躓いてツールを使う事をためらったり、”るつぼ”に嵌るようでは本末転倒です。
最低限だけ知っておいて、うまく付き合い、使いこなしていきましょう!
我々の本分はツールを使って成果を出す事なのですから。




コメント