統計における”ばらつき”の指標には、色々なものが存在します。
標準偏差、変動係数、分散、四分位偏差・・・
その中で、標準偏差と似たような名前で標準誤差というものがあります。
一瞬書き間違えかなとも思える名称ですが、標準偏差とは別に存在する指標です。
実はこの値、研究開発においては標準偏差よりも使い道がある値なんです。
今回はそんな標準誤差を標準偏差と比較しながら解説していきます。
研究開発や技術を営んでいる方はぜひ、覚えて使いこなせるようになりましょう。
標準偏差と標準誤差の特徴

まずは、それぞれの値の特徴に注目してみましょう。
標準偏差の特徴
標準偏差は以下の数式で表現される統計量です。
$$σ=\sqrt{\frac{\sum_{i=1}^{n}{(x_i-\overline{x})^2}}{n}}$$
詳しくは以下の記事を参照してください。
標準偏差の特徴は、個々のデータの”ばらつき”を表現しているという点です。
標準誤差の特徴
次に標準誤差の特徴です。
あるサンプルの標準偏差をσとした場合、標準誤差は以下の数式で表現されます。
$$SE=\frac{σ}{\sqrt{n}}$$
サンプルサイズnの平方根で標準偏差σを割った値が標準誤差なのです。
この標準誤差の特徴は、平均値の”ばらつき”を表しているという点です。
サンプルの平均値というものは、サンプルサイズが増えるほどに元の母集団の平均値に収束していきます。
これを中心極限定理といい、N(μ,(σ/√n)2)の分布をとります。
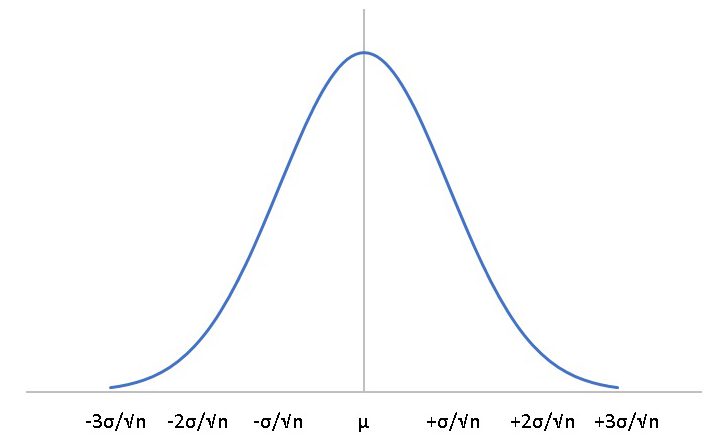
同じサンプルで比較してみよう
実際に以下のデータで、標準偏差と標準誤差を比較してみましょう。
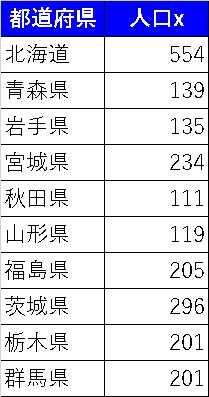
平均値、標準偏差、標準誤差を算出すると以下になります。
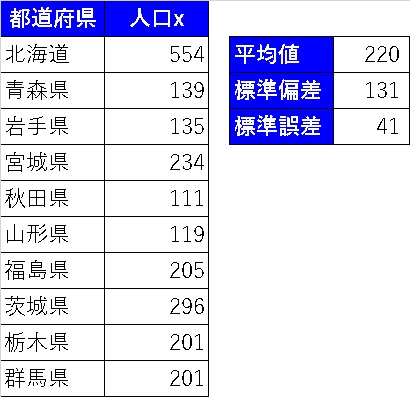
グラフにすると、
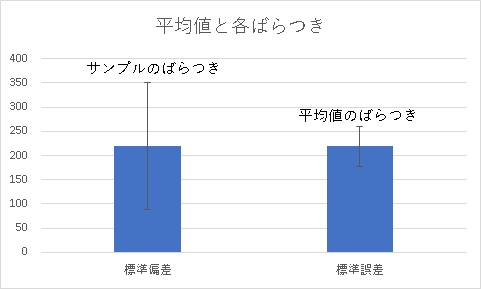
このように、標準誤差は標準偏差を√nで割るために、必ず標準偏差より小さくなります。
そして標準偏差と標準誤差が表しているものを、再度まとめますと、
・標準偏差:個々のデータのばらつき
・標準誤差:データの平均値のばらつき
ここがポイントです。
標準偏差と標準誤差の使い分け
標準偏差と標準誤差の特徴は分かって頂けたと思います。
次に、どのようなシチュエーションで使い分けるのかを紹介します。

標準偏差が望ましい場合
サンプル一つ一つの”ばらつき”を捉えたい場合は標準偏差を使用します。
例えば、製造現場での良品の管理基準を設ける時などです。
標準偏差と平均値を併用する事で、正規分布に則った管理が出来るので、合理的に管理基準を設ける事が出来ます。
詳細は以前にアップしていますので、こちらをご覧ください。
標準誤差が望ましい場合
平均値は基本的に、実験データの代表値として使用されることが多いです。
故にその実験の代表値がどの程度ばらつくのかを知りたい場合は、標準誤差を利用した方が良いです。
また、標準誤差をエラーバーとして平均値同士を比較する場合、上限と相手の下限値が振れない場合は2σ分離れるために、簡易的な有意差検定として機能させることも出来ます。
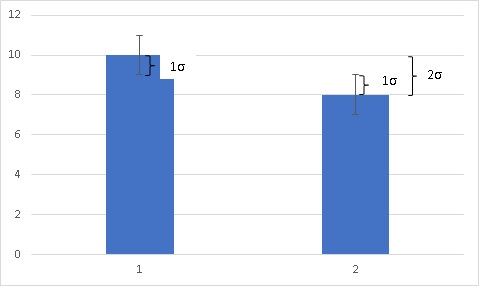
そもそも平均値の有意差検定の検定統計量の式は
$$z=\frac{\overline{x}-μ}{σ/√n}$$
であり、以下の分布上で2σ離れるという事は、ほぼ5%以下の確率でしか同じ分布とはなり得ないという事。
つまり有意差ありとなるラインなのです。
だから標準誤差のエラーバーで上下限が接しないほど平均値が離れている場合は、有意差ありと一目で判断することが出来るのです。
この辺りの詳細については、以下の記事もご覧になってください。
まとめ
標準偏差と標準誤差は名前だけでなく、数式もかなり似通っていますが、示したい情報は全く異なります。
標準偏差は個々のばらつき
標準誤差は平均値のばらつき
をそれぞれ示します。
故に標準偏差を使うなら、現場管理の管理値を決めるのに有効です。
一方標準誤差を使うなら、実験データの平均値の範囲や有意差を知る時に有効になります。
この辺りをはっきり区別して、使い分けを行い、他より抜きんでたデータ分析を実施していきましょう。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。





コメント
[…] 標準誤差についてもっと知りたい場合はリンクなどを見てください […]