標準偏差に必要なサンプルサイズはいくらか？

“ばらつき”を扱うツール、統計学

その中で最も重要な代表値が標準偏差です。

しかしながら、『標準偏差を知るために適切なサンプルサイズは？』と言われると実はよく分からないという事、ありませんか？

ネットで調べてるとN=30だのN=50だの、はたまたN=100は必要だの様々です。

これでは埒が明きません。

故に今回は、サンプルサイズがどの程度必要なのか、推定からの逆算で考えてみましょう！

youtubeでも解説しています。

品質管理のための統計学

posted with ヨメレバ

川野常夫 技術評論社 2012年07月

楽天ブックス

Amazon

Kindle

推定から逆算してみよう

なぜ推定から考えるのか？

推定とは、代表値(平均値や分散)がどの程度の確率(大抵95%)で、どの程度の範囲に収まるのかを導く手法です。

そして推定では、基本的に有意水準αを決めてしまえば、変数の要因はサンプルサイズしか残りません。

これは、ある信頼区間に収めたいのならば、このくらいのサンプルサイズが必要であるという事を逆算で導き出すことが出来る事を意味します。

分散の区間推定

区間推定とはある代表値(平均値や分散、標準偏差など)が、どのくらいの確率でどのくらいの範囲に収まるかを推定する技法です。

今回は標準偏差を話題として挙げていますが、推定の手法で扱われる”ばらつき”の指標は分散であるために、まずは分散の推定について考えてみます。

分散の推定については、以下の記事を参照ください。

• ばらつきを予測しよう！【カイ二乗分布による標準偏差の推定】

分散の信頼区間は以下になります。

$$1-α=Pr[X^2(n-1,1-α/2) ≦ X^2 ≦ X^2(n-1,α/2)]$$

↓

$$1-α=Pr[X^2(n-1,1-α/2) ≦ \frac{S}{σ^2} ≦ X^2(n-1,α/2)]$$

↓

$$1-α=Pr[\frac{S}{X^2(n-1,α/2)} ≦ σ^2 ≦ \frac{S}{X^2(n-1,1-α/2)}]$$

ちなみにX²はカイ二乗値です。

1-αは通常95%を設定します。つまりこの区間にσ²が収まる確率は95%ということです。

ちなみに上限と下限をそれぞれ平方根をとると、そのまま標準偏差の信頼区間となります。

信頼区間の比を見てみよう

今回はこの分散の上下限の信頼区間比の平方根、つまり標準偏差の信頼区間比がサンプルサイズによって、どのような推移を辿るのか見てみましょう。

この信頼区間の比は、

「このくらい標準偏差は振れるよ」

という意味になり、そのまま値の精度に繋がる数字となりますから、この値が1に近いほど精度が良いという意味になります。

先程得られた式、

$$1-α=Pr[\frac{S}{X^2(n-1,α/2)} ≦ σ^2 ≦ \frac{S}{X^2(n-1,1-α/2)}]$$

に対して有意水準α=0.05と設定すると、信頼区間の上下限の比は

$$\sqrt{\frac{X^2(n-1,0.025)}{X^2(n-1,0.975)}}$$

以上のような式で表現されます。

ここからは、エクセルの力を借りましょう。

エクセルで、自由度(⇒サンプルサイズn-1)と確率(⇒1-有意水準α)からカイ二乗値を導く関数は

=CHIINV(自由度、確率)

になります。なので、先述の標準偏差の信頼区間の比は

$$\sqrt{\frac{CHIINV(n-1,0.025)}{CHIINV(n-1,0.975)}}$$

でエクセルで計算することが出来ます。

どのくらい必要なのか考えてみよう

実際に計算してみました

結果が以下のグラフです。

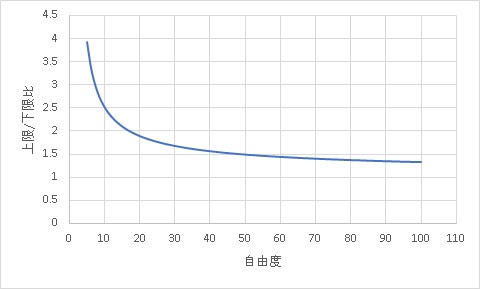
これで見てみると、自由度(≒サンプルサイズ)30程度から信頼区間の比の変化が落ち着きだしています。比としてはこの時点で1.66です。

少なくともサンプルサイズ20程度では、信頼区間の比(=1.86)がまだ大きいように見受けられます。

サンプルサイズ100になると、1.32になります。

結局結論は？

結局結論はどうなんだ？という声が聞こえてきそうですが、正直な話

「状況による」

としか答えられません。なんか申し訳ないです。

しかしながら、標準偏差を始めとした代表値がどの程度の精度で必要なのかは、やはりその状況によるのです。

少なくとも、推定から逆算することでサンプルサイズがどの程度精度に影響するのかは明白になります。

自分の観測データには、どの程度の標準偏差の精度が必要なのか。

上司はどの程度の精度なら許容してくれるのか。

なぜサンプルサイズを、この数で設定したのか。

今までは、

「一般的にサンプルサイズが30が妥当と言われている」

としか言えなかったのが、

「サンプルサイズ30とすることで、上下限比1.66に95%の確率で収まる」

と根拠をもって提出出来るようになります。

これは、とても大きな事だと私は思います。

まとめ

信頼区間の考え方を変形すれば、標準偏差や分散に必要なサンプルサイズを設計することが出来ます。

この方法を活用するメリットとしては、得られた標準偏差がどの程度当てになるかを予測することが出来るという点です。

測定対象の変動スケールを考慮すれば、必要最小限のサンプルサイズに抑えることも出来るし、逆にサンプルサイズが足らないということも防ぐことが出来ます。

コンテンツ紹介

昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。

そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。

しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。

そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。

youtubeでは登録者1万人の統計学のチャンネルを運用しています。

熊野コミチの統計とお仕事チャンネル

動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。

youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。

メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)

エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。

本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)

「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」

そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。

私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。

私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。

統計学を活かす 解析しやすい数値化のノウハウ

「いや、その前に使える手法を体系的に学びたいんだけど」

そんな方には、udemyの講座を推奨します。

メーカーの現役技術者による研究開発のための統計学

初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。

どの手法が結局使えますのん？という方はぜひこちらをお求めください。

こんな感じで、様々なコンテンツを展開しています。

今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。

ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。

twitter