私たちは小学生のときから様々なグラフを学習します。
棒グラフ
線グラフ
円グラフ
等々。
そんな中、学校では習わないグラフというのもあります。
その習わない中でも、非常に便利なグラフが箱ひげ図というものです。
今回はこの箱ひげ図を解説します。
このグラフは一つのグラフ中分布を複数個表現出来るものであり、使いこなせると様々な場面で役に立つのでぜひ習得してください。
動画でも解説しています。
箱ひげ図は何を示してくれるのか?
まず分布を表現してみよう。
箱ひげ図の前にまず、分布をグラフ化するという事を思い描いてください。
おそらく、普通に浮かぶのは以下のようなヒストグラムだったりするはずです。
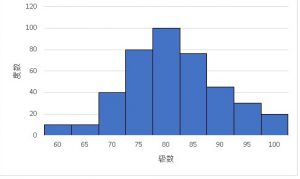
様々な形状の分布を表現できるヒストグラムですが、一つ欠点があります。
分布同士の比較がうまく出来ないという事です。
この理由としては、一つのグラフ中に一つの分布しか表現できないために、どうしても同じスケールで比較出来ないという事が考えられます。
逆を言えば、分布同士を比較するためには一つのグラフ内で分布を複数表現する必要があるという事です。
箱ひげ図は分布をいくらでも表現出来るグラフ
箱ひげ図と呼ばれるグラフで以下のような形をしています。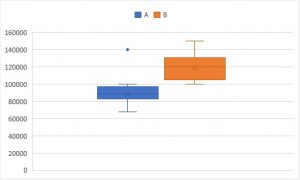
箱ひげ図という名前が示すように、箱部分とひげ部分によって構成されています。
そしてこの箱+ひげで表現される図一つ一つが分布を表しています。
つまり上記のグラフは、青の分布とオレンジの分布を比較しているグラフになるのです。
そしてここで示したグラフから、以下の情報が読み取れます。
・AとBは分布の中心の値に根本的に差がある
・Bの方がばらつきが大きい
・Aは小さい側、Bは大きい側に若干分布が偏っているが分布の対称性は良好
・Aには1点外れ値がある。
これらの情報が一枚のグラフの中ですべて表現されているのです。
通常これだけ1つのグラフ内で情報量が多いものも稀です。
というわけで、これから箱ひげ図の構造を見ていきましょう。
箱ひげ図の構造を見ていこう
箱ひげ図を表す5つの数字
箱ひげ図は主に四分位数によって構成されたグラフです。
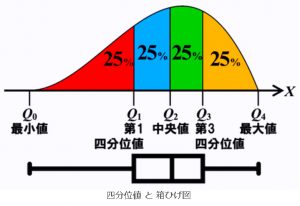
四分位数とは、名前の通り数字の集団を大きな順(もしくは小さな順)に並べた場合、ちょうど四分割にするように位置する数値を指します。
四分割にするなかで小さい方の数値を第1四分位値
四分割するなかで真ん中に位置する数値を第2四分位値
四分割にするなかで大きい方の数値を第3四分位値
といいます。そして第2四分位数は中央値そのものです。
図のように四分位数で箱の部分が構成されます。
箱の下端が第1四分位数
箱の中央の線が中央値
箱の上端が第3四分位数
ばらつきが大きくなると、箱のサイズが大きくなります。
以下のグラフを見て下さい。
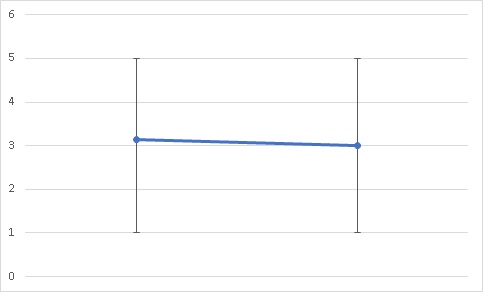
エラーバーは最大及び最小を示しています。
これを見ると、二つのグラフはほぼ同じ分布のように見えます。
ですが、以下のように箱ひげ図で表すと
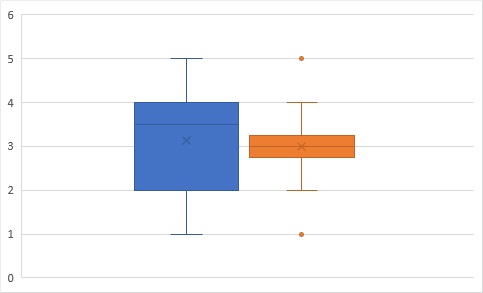
このように箱のサイズが全然違います。つまり最大、最小値が同じでもばらつきは全然違うのです。
このように最大値と最小値が同じ分布でも、箱を比較するとばらつきが全然違うということはよくあります。
次に分布の偏りについてです。
分布に偏りが無い場合は、中央値を中心に箱の下端と上端の位置は均等になるのですが、偏りが生じているとそこの部分が長くなります。
例えば数値の大きな方に分布が偏っている場合(ヒストグラムだと右側に分布の裾が広がる場合)、箱の中心線から箱の上端の長さが、中心から下端までの長さより長くなります(以下の図参照)。
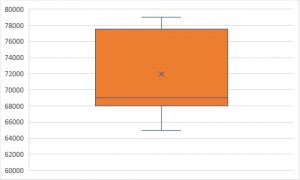
最後にひげについてです。
最大値、最小値を四分位数の第一、第三から伸ばすとそれがひげに相当する部分になります。
以上で箱ひげ図を構成する最低情報は揃いました。
しかしながら、これだけではまだ不十分です。
更に情報量が多いグラフにするためには、四分位範囲と平均値を加える必要があります。
四分位範囲とは
第三四分位数と第一四分位数の差のことを四分位範囲(以下IQR)と呼びます。
箱部分の縦の長さのことです。
$$第三四分位数-第一四分位数=四分位範囲(IQR)$$
そしてここからが重要なのです。
先程箱の上端、下端から最大値、最小値までを引っ張るとひげになると述べました。
しかし、分布外れの値(つまり外れ値)を表現するために、ここに一つ条件を加えます。
箱ひげ図の上端もしくは下端から1.5×IQR分の範囲に収まる中での最大値、最小値までにひげを引くという条件を加えます。
以下の図を見て頂くとイメージが湧くと思います。
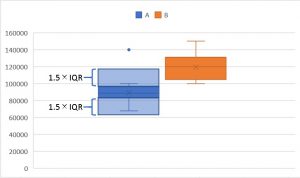
ここの範囲を出た数値は、外れ値として検出されることになります。
また平均値も箱ひげ図に記載すると、中央値と平均値の比較ができます。
以前紹介したように、分布に偏りが生じた場合中央値と平均値に差が生じる可能性があります。
詳細は以下の記事をご覧ください。
- 投稿が見つかりません。
ちなみに箱ひげ図における外れ値が発生する確率については、以下の記事をご覧ください。
標準正規分布を元にした値にはなりますが、参考になると思います。
まとめ
箱ひげ図は、分布を比較することが出来るグラフです。
箱ひげ図から拾える情報は以下になります。
・中央値と平均値のズレから分布の偏りが分かる
・箱の偏りで分布の偏りが分かる
・箱のサイズでばらつきが分かる
・外れ値が分かる
これだけの情報を一つのグラフの中で複数の分布について比較出来ます。
これほど情報量の大きい単一のグラフというのは他にありません。
一見すると分かりづらいグラフですが、一度読み方が分かると非常に心強い味方になります。
また作図も最新のエクセルには標準で装備されているので簡単にできます。
本当に便利なので皆さんどんどん使っていきましょう!



コメント