皆さんは何かを測定する場合、あまり1回で測定を済ませることは無いですよね?
きっと、複数回測定してその平均を採用すると思います。
なぜなら、データがばらつくからです。
ですが、ばらつくのは測定データだけではありません。
平均値や標準偏差などの統計量もばらつきます。
おそらく言われるまでもなく、この事はよく分かっていると思いますが、結構見て見ぬふりをしているのではないでしょうか?
このような統計量のばらつきに対処するテクニックとして、区間推定というものがあります。
今回はこの区間推定について母分散既知の平均値の推定を例にとることで解説いたします。
動画でもアップしています。
区間推定とは何か?

統計量の区間を推定する手法
区間推定とは、読んで字のごとく区間を推定する手法です。
先述したように統計量はばらつきます。
測定したデータがばらつくので、それを計算して得た統計量がばらつくのは当然です。
ただし”ばらつく”といっても無作為にばらつく訳ではありません。
ある分布に従ってばらつきます。
平均値の場合は正規分布やt分布に従いますし、分散の場合はカイ二乗分布に従います。
この性質を利用する事で、統計量がばらつく範囲を予測する事が出来ます。
推定の手順
推定は主に以下の手順で行います。
1,統計量(平均値,分散)を求める
2,統計量の標準化を行う
3,95%信頼区間を求める
4,標準化した統計量を式変形して元の統計量の区間を導く
フローが決まっているという点は、検定と似たものがあります。
文にすると、分かりづらいので平均値の区間推定(母分散既知)を例にとって実際にやって見ましょう。
母分散既知の平均値区間推定
今回は母分散既知の平均値区間推定をやってみます。
母分散既知は、大標本でなければ適用出来ませんが、正規分布を使った検定ということもあって理解がとてもしやすいので、推定の学習においては一番最初に行われる手法になります。
まずは
1,統計量(平均値,分散)を求める
以下のデータを使っていきます。

とりあえず全ての測定値の平均値を出してみます。
結果としては
平均値=4.3
になりました。次は2,統計量の標準化を行う
平均値の標準化は以下の式で行います。
$$\frac{\overline{x}-μ}{\frac{σ}{\sqrt{n}}}$$
とりあえずは母分散が既知であるということで、この表から求められる標準偏差を使用します。
標準偏差:3.0
よって標準化すると、
$$\frac{\overline{x}-μ}{\frac{σ}{\sqrt{n}}}=\frac{4.3-μ}{\frac{3.0}{\sqrt{10}}}$$
になります。ここでなぜ標準化を行うのかと言いますと、平均値を標準化すると標準正規分布に従うという性質があるためです。
この性質を利用する事で、標準正規分布表を使用して区間推定を行う事が出来るのです。
次に3,95%信頼区間を求める
平均値の標準化した値は、標準正規分布に従うので標準正規分布表を確認してみましょう。
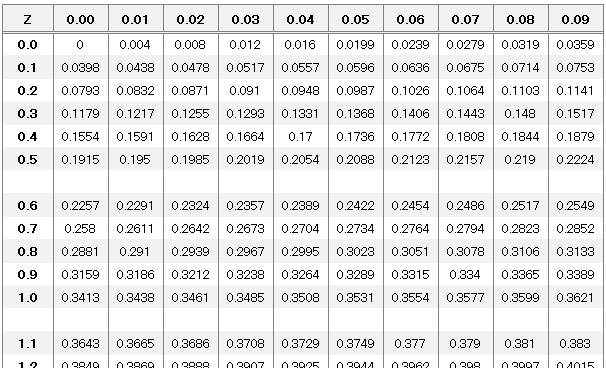
今回の場合、0.475になるz値を見つけます。標準正規分表には分布の片側しか載っていないからです。0.475を2倍するとちょうど0.95になります。
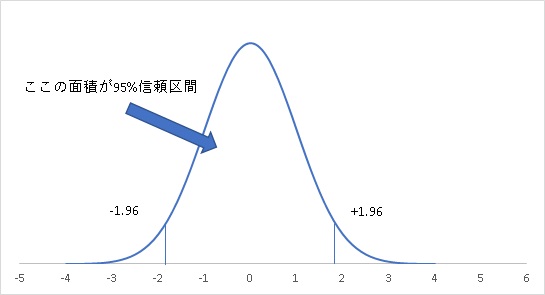
ちなみに、エクセル関数の
NORM.INV(確率,平均値,標準偏差)
で確率を0.975(もしくは0.025)、平均値を0、標準偏差を1にしても同じ値(1.96)を得られます。
よって、標準化した平均値は以下の範囲に収まります。
$$-1.96 < \frac{4.3-μ}{\frac{3.0}{\sqrt{10}}} < 1.96$$
そして最後に、4,標準化した統計量を式変形して元の統計量の区間を導く
先程の不等式を変形すると以下になります。
$$4.3-1.96×\frac{3.0}{\sqrt{10}} < μ < 4.3+1.96×\frac{3.0}{\sqrt{10}}$$
$$2.4 < μ < 6.2$$
母平均はこの区間内に95%の確率で収まることがわかりました。
推定の豆知識

エクセル関数で算出出来る
色々と面倒な工程が多いですが、エクセル関数で簡単に算出出来ます。
=CONFIDENCE.NORM(α,標準偏差,サンプルサイズ)
これで、信頼区間の範囲が出ます。
サンプルの平均値に対してこの関数の値をプラスすれば上限、マイナスすれば下限が出ます。
標準偏差とサンプルサイズで変動する
信頼区間が狭いほど、予測は高精度といえます。
この信頼区間を左右するのは、標準偏差とサンプルサイズです。
標準偏差が小さいほど、そしてサンプルサイズが大きいほど信頼区間が小さくなります。
標準偏差は測定データのばらつきになるのですから、これが小さければ平均値の精度が高くなることは当然です。
サンプルサイズに関しては、測定個数が増えれば増えるほど、平均値(もとい統計量)の精度が上がるので、感覚的には理解しやすいと思います。
そもそも、サンプルサイズが増えると精度が高くなるという現象をこの標準化の式は表しています。
このように、平均値の精度を上げたい場合、標準偏差を小さくすることが難しければ、測定するサンプルの数をどんどん増やしていけば良いという事になります。
まとめ
今回は区間推定の代表例として母平均の推定を紹介しました。
ポイントとしては、
・標準化
・分布で信頼区間を確認
・母平均μの範囲を算出するように、式を変形する
です。
今回の事例は、母分散既知という大標本(数十以上)を想定した例であり、サンプルサイズ10個前後の少数の場合には適用できません。
小標本の場合は、t分布を適用した手法を使う必要があります。
その例に関しては以下の記事に書いていますので、ぜひ参照してみて下さい。





コメント