皆さん平均値というものはご存知ですよね?
では、なぜ平均値というものを算出するのか今一度考えてみましょう。
体育館の中で、同じ紙飛行機を同じ人が投げた場合毎回同じ飛距離になるでしょうか?
当然同じ飛距離にはなりません。
ある程度”ばらつき“ます。
通常この”ばらつき”の情報は邪魔です。ゆえにこの“ばらつき”を排除した値が平均値になります。
ですが、時にはこの”ばらつき”そのものの情報が欲しい場合もあります。
この“ばらつき”そのものを表した値の代表格が標準偏差です。
統計学への理解は、まずこの標準偏差の理解から始まると言っても過言ではありません。
しかし、この標準偏差は統計学の最初のつまづきポイントと言われるくらい分かりにくい概念です。
今回はそんな標準偏差をポイントを押さえながら、分かりやすく解説いたします。
動画解説もアップしていますので、こちらもぜひご覧ください。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
標準偏差を理解しよう!

標準偏差の式は以下のようになります。
$$標準偏差=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\overline{x})^2}}$$
こうしてみると、式がややこしそうです。
この上そもそも”ばらつき”というものを普段考える事が少ない為、苦手意識を持つ人が多いのも頷けます。
ですが、以下の3つのポイントを押さえていけば必ず理解出来ます。
・偏差
・偏差平方和
・分散
これらの値を理解していくと、標準偏差をすんなり理解出来るようになります。
まずは偏差からです。
偏差とは何?
まず偏差という数字を理解しましょう。
例えば先の紙飛行機の飛距離が例えば以下の通りだったとします。

各投目平均値とは一致せず、ばらついています。
偏差とは各値と平均値との差の事です。
つまり、1投目の場合偏差は
$$偏差=3.00-4.75=-1.75$$
となります。
これまで言及してきた”ばらつき”とは、この偏差の事を指していたのです。
そして標準偏差とは、この偏差を平均化した値なのです(厳密にはちょっと違います。詳細は後述)。
この偏差を一般的な式で表現すると、
$$偏差=x-\overline{x}$$
になります。
先程の表の全ての偏差を算出すると

このようになります。グラフでも見てみましょう。
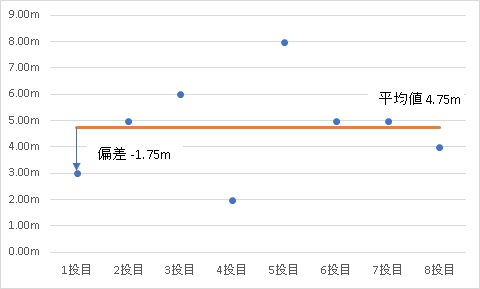
これが個々の”ばらつき”偏差です。
次にこの偏差の平均化を試みてみましょう!
なぜ偏差平方和を求めるの?
さぁ先ほどの偏差を平均化してみましょう!
そうすることで、偏差の代表値が出せるハズ・・・
あれ?0になった。今回は標準偏差は0なのか?

いえ、そうではありません。実は偏差は平均化する事が出来ないのです。
これは、式で読み解くと納得しやすいです。
偏差の平均値を一般的に表すと
$$\sum_{i=1}^{n}{(x_i-\overline{x})}=nx_i-n\overline{x}$$
ここで平均値![]() の式を思い出してください。
の式を思い出してください。
$$\overline{x}=\frac{1}{n}\sum_{i=1}^{n}{x_i}$$
この平均値の式の両辺にnをかけると、
$$n\overline{x}=n×\frac{1}{n}\sum_{i=1}^{n}{x_i}=\sum_{i=1}^{n}{x_i}=nx_i$$
となり、結局nxiもn![]() も同じ値なので引き算すると0になるわけです。
も同じ値なので引き算すると0になるわけです。
という事で、偏差は平均化する事が出来ません。
何か一工夫する必要があります。
これを解決する発想は、意外と単純です。
2乗して、全て正の値にしてしまえばいいんです。
そもそも、”ばらつき”方に正と負が混じっていたことでプラスマイナス0になってしまっていたので、じゃあマイナスを無くせばいいんだという事ですね。単純明快です。
この事から分かるように、統計学における”ばらつき”とはばらついている方向に対しては考慮していません。
プラス側だろうが、マイナス側だろうが関係なく、重要なのはどのくらいばらついているかなのです。
向きではなく、大きさが重要なのです。
では、紙飛行機の偏差を2乗しましょう。
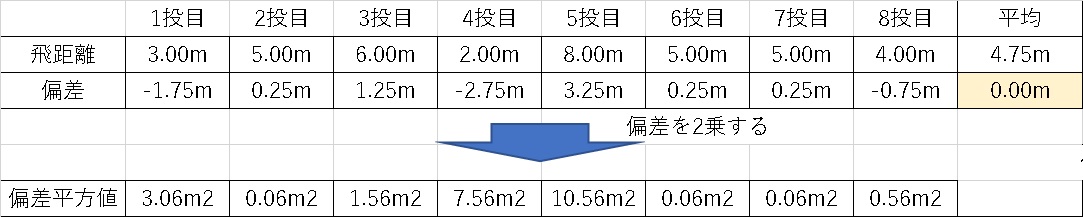
そして、この偏差を平方した値の平均値を求めるには、まず総和させる必要があります。
$$偏差平方和=\sum_{i=1}^{n}{(x_i-\overline{x})^2}$$
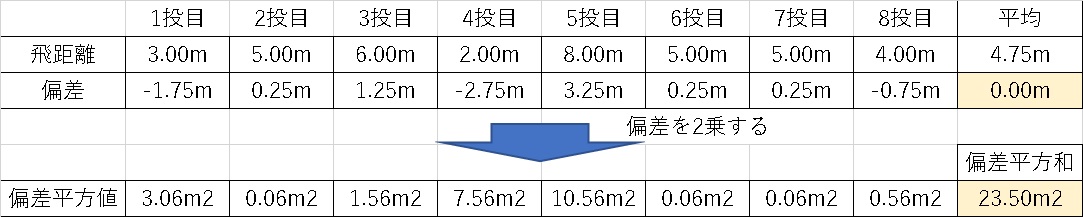
これが偏差平方和です。
総和を求めたら後は、足した個数で割るだけで平均値が出ますね。
分散と標準偏差
偏差の平均値(みたいなもの)を求めるために、偏差平方和を求めました。
後は足し合わせた個数で割れば、偏差の代表値が出せそうです。
$$分散=\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2}$$
「ん?分散?標準偏差じゃないのか?」
そうです。偏差平方和をサンプルサイズで割った値は分散と呼ばれる数字で、標準偏差ではありません。
実は分散からもう一つプロセスを踏まなければ、標準偏差にはなりません。
その最後のプロセスとは、平方根をとることです。
それはなぜか?
もう一度思い出し得て頂きたいのですが、偏差を総和させる段階で符号を正に統一するために2乗する処理をしています。
なので、当初値と単位が異なり、2乗になっているのです。
さりげなく表にも書いていましたが、紙飛行機の飛距離も2乗のm2になっています。
元の値と同様に扱う(特に平均値と一緒に扱うには)、平方根をとって元の単位に戻してやる必要があります。つまり
$$標準偏差=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2}}$$
これが標準偏差です。
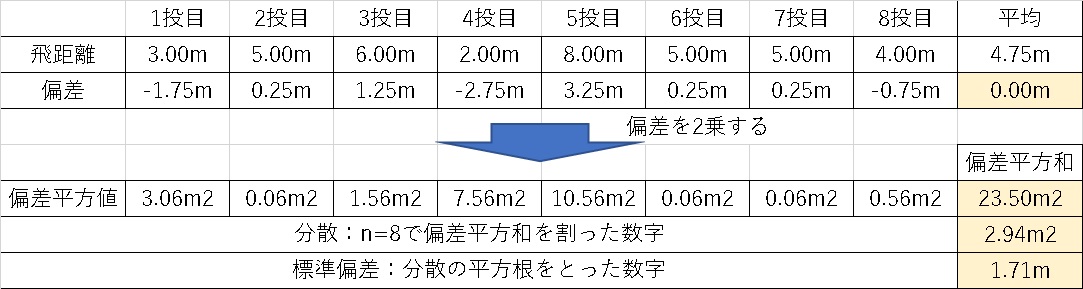
やっとたどり着きました。
これで、標準偏差つまり測定した値の”ばらつき”を取り扱う事が出来ます。
標準偏差を扱う上での注意点

標準偏差は”ばらつき”の最も重要な代表値です。
ですが、この値を扱う上でいくつか注意点があります。
nで割るかn-1で割るか
実は標準偏差は知りたい対象が、
・母集団のばらつき
・採取したサンプルのばらつき
のいずれが知りたいかで、nで割るかn-1で割るかが変わってくるのです。
計算した集団そのもののばらつきを知りたい場合はnで割り、計算した集団の母集団のばらつきを知りたい場合はn-1で割ります。
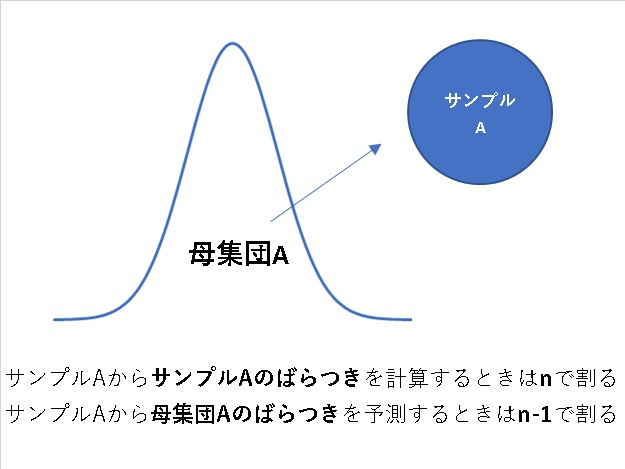
なぜ、状況に寄ってnで割ったりn-1で割るのかは以下の記事を参照ください。
標準偏差は単純に比較するのには向かない
標準偏差は直接比較するには、あまり向いていません。
それは、平均値の増大に伴って標準偏差も大きくなる性質を持っているからです。
例えば
・500gの分銅の標準偏差100g
と
・5kgのダンベルの標準偏差500g
だと、どう考えても実感的にはダンベルのばらつきの方が小さく感じますが、単純に比較すると分銅の標準偏差の方が小さいのでばらつきが小さいとなってしまいます。
このような場合、変動係数という値を使うのが適切です。
このように標準偏差に向かない取り扱いもあります。
詳細は以下の記事をご覧ください。
標準偏差は直接足し算や引き算できない
標準偏差は直接足し算、引き算をする事が出来ません。
なので、標準偏差100の材料と標準偏差20の組み合わせたら標準偏差は120になるとはならないのです。
ですが、ばらつきを持った材料同士を組み合わせたときのばらつきというものを知りたいシチュエーションもあると思います。
このような場合、一度分散にする(つまり2乗する)と足し算、引き算する事が出来ます。
つまり先の標準偏差100と20を組み合わせた場合、
$$組み合わせ後の標準偏差=\sqrt{(100^2+20^2)}≒102$$
となります。単に足し算した値とかなり異なるという事が分かると思います。
実はこの分散性質はかなり重要であり、統計で様々な数学的処理を行う際は標準偏差より分散が多用される理由でもあります。
この分散の加法性に関しては以下の記事を参照ください。
エクセルでの算出法

今回紹介した標準偏差。手計算でやるにはかなり面倒です。
各値を平均値で引いて、それぞれ2乗するなんてやってられません。
ですが、安心してください。
エクセルには標準偏差を算出する関数が配備されています。
ここでは以下に様々な関数を紹介します。
・母集団を予測する場合(n-1)では
=STDEV.S(数値1,数値2,…)
・サンプルそのものの標準偏差を計算する場合(n)では
=STDEV.P(数値1,数値2,…)
ちなみに、
・母集団の分散を計算する場合(n-1)は
=VAR.S(数値1,数値2,…)
・サンプルそのものの分散を計算する場合(n)では
=VAR.P(数値1,数値2,…)
で算出出来ます。
覚えておくと便利ですよ。
まとめ
今回は統計学において最も重要な値である、標準偏差を紹介しました。
これを理解する上で重要なのは、
・偏差
・偏差平方和
・分散
の3つの値です。
標準偏差の式の導出の過程をこの3ポイントを押さえながら追いかけていくと、理解しやすいです。
また、標準偏差は平均値と違って扱う上でいくつかの注意点がありますので、この点を気をつけながら使っていきましょう。
標準偏差は特に正規分布と組み合わせて使うと、実務上でもかなり高い効果を発揮します。
この標準偏差を皮切りに、統計学を学んでみて下さい。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ!」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます!!
買い切りタイプなのでお得です。
ぜひお求めくださいな。





コメント